A linear number sequence (aka arithmetic sequence) is an ordered set of numbers which has a common (constant) difference between consecutive terms.
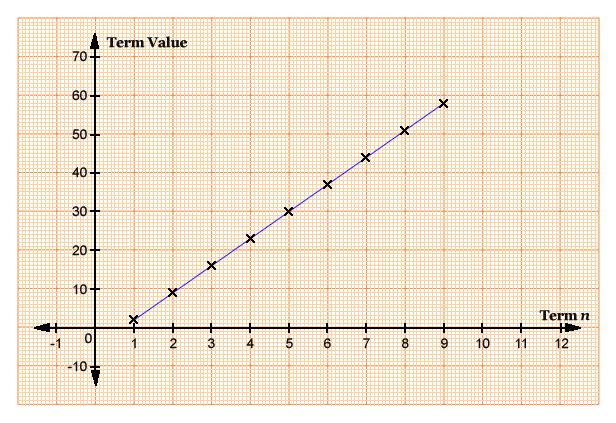
Consider this linear number sequence: 2, 9, 16, 23, 30, 37, 44, 51, ....

Term
Each number in a sequence, separated by commas, is called a term of this sequence. The first term is called T1, followed by T2, T3, and so on.
Term Value
In a linear number sequence, the term value is the number value of one term. In above example the term value of T6 = 37.
Common Difference
The value added between each consecutive term is called the common difference and is always constant in any linear number sequence. We use the letter d to represent the common difference. The common difference can be a positive or negative value.
In above example, the common difference equals 7.
Finding the Next Term
The rule for finding the next term is to add d (common difference) to the previous term:
Tn+1 = Tn + d.
In above example, the rule for finding the next term is to add 7 (common difference) to the previous term, e.g.
T9 = T8 + 7 T9 = 51 + 7 T9 = 58.
Finding the nth Term
The nth term (Tn) of a linear number sequence allows to calculate any term of the sequence:
Tn = d × n + T1 - d.
We can now work out any term for above example. E.g. the 40th therm:
T40 = 7 × 40 + 2 - 7 T40 = 280 + 2 - 7 T40 = 275.
Graphing Linear Number Sequences
We can graph the term on the x axis and the term value on the y axis. Joining all the points will result a linear (straight) line.
Graphing above example: